 |
| Artist impression of SWARM (image: ESA) |
When I started tracking satellites and publishing this blog 18 years ago, I spent a lot of time on validating the accuracy of my methods and observations. A lot has happened since then: I moved on to better equipment, and new validation methods have become available.
In this blogpost, I revisit the accuracy of my current video observations, using ESA's SWARM satellites as calibration targets.
The SWARM satellites (2013-067A, B and C) are well suited for system validation. Accurate GNSS-fit based orbital positions with centimeter accuracy are publicly available for these satellites, which means there is a firm reference to compare to. And the SWARM satellites are quite bright, hence they are relatively easy to observe (the video below shows a pass of SWARM A on 27 March 2023, imaged with a 85 mm lens).
Observations, equipment and methods
From the last week of March 2023 to the 3rd week of April 2023, I targetted SWARM A and B while they were making a series of well-observable passes over Leiden.
There were two reasons for this endeavour. One was the creation of a good tracking dataset with known 'ground truth" for our research at Delft Technical University, where a colleague is working on improved methods of orbit determination from optical observations. The second was, that such observations provide you with information on the astrometric accuracy of various camera/lens combinations.
My previous endeavours to gain insight into the accuracy of my observational data were based on comparisons of observations to TLE's. True vector positions from fitting to data from GNSS receivers onboard the satellite(s) are however much more suited for this than TLE's, as they are much more accurate (to cm-level, whereas those of a TLE are to km level).
The equipment I used to obtain the data presented in this blogpost was a WATEC 902H2 Supreme camera with a GPSBOXSPRITE-2 GPS time inserter, and three lenses: a Pentax 1.2/50 mm, a Samyang 1.4/85 mm and a Samyang 2.0/135 mm. Astrometry on the imagery was done on a frame-by-frame basis using Hristo Pavlov's TANGRA software.
| WATEC 902H2 Supreme camera with Pentax 1.2/50 mm lens and GPS time inserter |
| same camera as above but with 2.0/135 mm lens |
The camera films at 25 frames/second. The PAL video signal is fed into the GPS time inserter, which imprints each frame with a millisecond-accuracy time marking. The signal is then fed into an EZcap digitizing dongle and recorded on a laptop, after which astrometry is done on the files with TANGRA, on a frame-by-frame basis.
Observations were done on 8 separate nights in the period 27 March-19 April 2023. 1544 datapoints from 3 separate passes were obtained with the 50 mm lens; another 4100 datapoints from 5 separate passes with the 85 mm lens; and 891 datapoints from 3 separate passes with the 135 mm lens.
In addition to this, Cees Bassa and Eelke Visser both provided a set of data from their video systems. This allowed to explore any differences between their equipment and mine.
Cees and Eelke use USB connected ZWO ASI camera's with a CMOS sensor. Cees' camera is a ZWO ASI 1600 MM with a 1.4/85 mm lens; and Eelke's camera is a ZWO ASI 174MM with a 1.4/50 mm lens.
Their timings come from the PC clock which is synchronized through NTP. Their astrometry is done using Cees' STVID software. As we will see later, there are some clear differences in accuracy between their systems and my system.
Reference positions
I wrote a software program, "Vect2RADEC', that converts SWARM navigational positions (ITRF X Y Z coordinates) to J2000 RA and DEC positions as seen from the camera location, and optionally also calculates residuals with astrometrical positions if you provide a file with the latter. The software is available in the software section of my website at http://software.langbroek.org (64-bits Windows only).
Results (1)
First, results for my own system using various lenses. Below are error distribution plots for the three lenses used: plotted is the distribution of the distance delta (in arcseconds) between the astrometrically measured, and actual GNSS derived position.
The first plot is a combined plot, followed by plots per lens. The average accuracy, and the one sigma standard deviation on this, is listed in the plots as well.
 |
| combined plot of error distributions |
For each lens, the average accuracy is clearly better than the one-pixel resolution of the camera/lens combo in question. These pixel resolutions are resp:
1 pixel = 35.4" for the 50 mm lens;
1 pixel = 20.9" for the 85 mm lens;
1 pixel = 13.1" for the 135 mm lens.
The actual astrometric accuracies are at about 2/3rd of this, i.e. astrometric positions are accurate to sub-pixel level.
The error distribition for the 50 mm lens is a normal distribution. Those for the 85 mm and 135 mm lens are increasingly skewed, showing a tail towards lower accuracies in their error distributions.
The tails to lower accuracy in the plots for the 85 mm and 135 mm lens are caused by trailing of the satellite in individual frames: at the resolutions of these lenses, trailing becomes apparent at shorter range to the camera. TANGRA does not center well on trails, the software is meant to fit on point-like objects.
The dependency of accuracy on range for the various lenses as a result of trailing is visible in these plots of error against range:
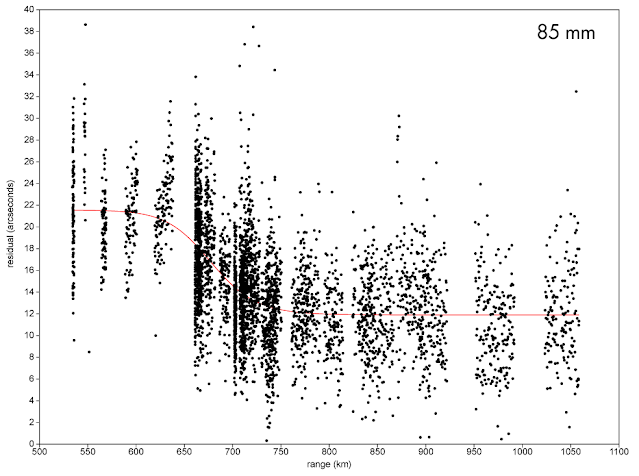
At the resolution of the 50 mm lens, trailing is not much of an an issue, even at minimum range: the error is constant. With the 85 mm lens, trailing (with a corresponding drop in accuracy) starts once the range is less than ~725 km. With the 135 mm lens, it starts as soon as the range is less than ~1200 km.
The following diagrams show the corresponding trends in actual error in meters at satellite range (perpendicular to the viewing direction), for the three lenses:
Results (2)
As a second investigation, it was interesting to compare the performance of my system to that used by Cees Bassa and Eelke Visser, who graciously made data available to me for this purpose.
In the diagram below, the distribution of residuals from Cees' system (green) is compared to those for my system (blue) for the same lens, a 1.4/85 mm Samyang lens. Cees' data (with a much lower number of individual datapoints) have been scaled on the Y-axis to visually match mine, in order to make the visual comparison of both distributions more easy.
What is immediately apparent is the difference in accuracy. The average error in Cees' results in a factor 6 worse than mine, and the distribution spreads much wider as well. It is also a factor 5 worse than the pixel resolution of his camera (whereas mine is at 2/3rd of the pixel resolution). Eelke's data, not visualized here, show a similar pattern.
The software which I wrote to assess these errors, currently does not
differentiate between along-track ("delta T") and cross-track errors. A
comparison of Cees' and my data against a TLE using Scott Campbell's
SatFit software, which does differentiate between delta T and
cross-track error (but only to two decimals behind the dot, in degrees
and time), suggests that much of the difference in error actually stems
from a larger along-track error, i.e. an error in the timing, in Cees' data.
This could have a couple of causes. One or more of these factors could be in play here:
(1) an uncorrected latency introduced by Cees' camera system;
(2) a latency introduced by the pc clock-to-STVID throughput of times
(3) a residual latency in the NTP time source
(4) the frame exposure mid-time registered by STVID might actually be the start- or end-time of the frames
(5) the frame stacking method used by STVID
NOTE: It should be explicitly remarked here that Cees never designed his system and software with the kind of precise accuracies in mind that we are mapping here.
In our independent tracking network focussing on orbit determination of classified objects, we generally are happy if positions reported are accurate to 2 arcminutes, rather than a few arcseconds. This is because of two reasons:
(a) The goal is to create TLE's for orbit characterization and overflight predictions for these objects. TLE's have an intrinsic accuracy of 1 km (and worse away from epoch time) in position, so a 2 arcminute accuracy in positional determinations is sufficient for this goal.
(b) Positional data of varying quality obtained by various different methods are lumped in the orbit determinations by our independent network analysts. These include: visual observations with binoculars and stopwatch; camera still images; video data with astrometry on either stacked frames or individual frames; with timing sources varying from stopwatch synchronization to radio "six pips", DCF77 radio-controlled clocks, to software synchronization to NTP time synchronization, to GPS time inserters.
NOTE ADDED 9 and 10 May 2023:
In a discussion on Twitter, the issue of light travel time was raised. I have come to the conclusion that this is almost certainly already included in the AFSPC-origin libraries I use for my software (even though not explicitly documented for the conversion of ECI position to RA/DEC as seen from the station, it is documented for another conversion, so likely to be incorporated in the former as well), for as I try to include my own additional correction, this actually makes the residuals worse.
Acknowledgement: I thank Cees Bassa and Eelke Visser for providing comparison data from their systems.









No comments:
Post a Comment